
在深入研究机器学习与深度学习之前我们需要了解一些基本概念,机器学习中的很多公式就是从这些基本概念和基本公式中推演发展出来的。同时我们还需要掌握基本的微积分和线性代数的知识,越到后面,公式的推演愈加复杂。
<h4>假设函数(The Hypothesis Function)</h4>
假设我们有一堆输入项:
以及输出项:
假设存在一个线性函数
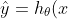=\theta_0 + \theta_1\cdot x)
能够精确地拟合这些输入项与输出项,那么这样的函数被称为假设函数(在统计学里可以被称为回归线吧)
假设我们有以下的训练集:
| inuput | output |
|---|---|
| 0 | 1 |
| 1 | 3 |
| 2 | 6 |
| 3 | 7 |
此时,我们假设第一个参数为1,第二个参数为2,则我们的假设函数为:
当输入值为2时,预测的输出值为5,但是实际值为6,因此我们尝试不同的参数组合来找出最为拟合这些训练集的假设函数。为了度量假设函数与训练集之间的误差,我们提出代价函数(cost function)的概念。
<h4> 代价函数(Cost Function)</h4>
我们可以用统计学中方差的概念来理解代价函数
这个公式实际上就是统计学中的方差公式,其代价函数的值越小,则假设函数与训练集拟合得越好,在以后的学习中,我们需要常常用到这个公式。
<h4>梯度下降算法(Gradient Descent Algorithm)</h4>
梯度下降算法是一种用来计算代价函数局部极小值的一种算法,在之后的研究中,梯度下降算法是一个大杀器。
由于假设函数是其参数
的函数(为方便讨论,我们暂时只考虑仅含有两个参数的hypothesis function),因此我们通过不断地修改这两个参数使我们的假设函数愈加地拟合我们的数据集,也就是说我们不断地使这两个参数的代价函数值越来越小。假设我们将cost function以这两个参数为自变量,其值为因变量绘制三维图,我们假设cost function的函数图像如下图所示:

假设图中小球所处的位置即我们在cost function上任意选择的一处位置,微积分的知识告诉我们,图中的小球会随着曲面的梯度不断下降(其梯度也在不断地变化),直到其下降到曲面的最低点。但是这个算法所算得的最小值很可能是曲面的局部最小值,关于这个问题的探讨可以在维基百科里看到。(传送门)
微积分的知识告诉我们,代价函数J关于这两个参数的梯度为:
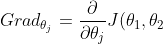,j=1,2)
因此其参数的变化可以这样表示:
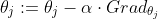
其参数α代表的是梯度下降的速率,因为计算机无法处理连续变化的值,因此我们只能用一些列变化较小的离散量来表示连续变化的值。
<h4>总结</h4>
以上就是入门机器学习及深度学习需要掌握的一些基础知识,想了解更多的话可以参考我写的构建神经网络来识别手写数字,或者Andrew Ng的线上课程:机器学习。