Calculate the trajectory of our cannon shell including both air drag and the reduced air density at high altitudes so that you can reproduce the results in the figure.Perform your calculation for different firing angles and determine the value of the angle that gives the maximum range.
Projectile motion
-
Newton's second law in two spatial dimensions

(1)
Euler method for second-order ODE
-
write each of these second-order equations as two firest-order differential equations
- finite difference form
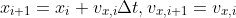
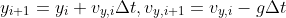
Resistance
-
the magnitude of the drag force is given by
which -
the componets of the drag force

(2)
- Euler method with resistance
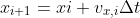
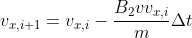
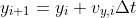
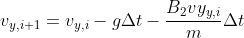
How to decide the point of fall?
-
the last point above the ground(n) and the first point below the ground(n+1) is given by
Code(python)
-
without air resistance
import numpy as np
import math
import matplotlib.pyplot as pl
class cannon_shell:
def __init__(self,time_step=0.1,total_time=30,gravity=9.8,initial_dis=0):
print("enter the angle of the cannon shell ->")
self.rad=float(input())
self.angle=(self.rad/180)*math.pi
print("enter the speed of the cannon shell ->")
self.velocity=input()
self.g=gravity
self.dt=time_step
self.v_x=[self.velocity*(math.cos(self.angle))]
self.v_y=[self.velocity*(math.sin(self.angle))]
self.x=[initial_dis]
self.y=[initial_dis]
def run(self):
while(self.y[-1]>=0):
self.x.append(self.x[-1]+self.v_x[-1]*self.dt)
self.y.append(self.y[-1]+self.v_y[-1]*self.dt)
self.v_x.append(self.v_x[-1])
self.v_y.append(self.v_y[-1]-self.g*self.dt)
def show_result(self):
pl.plot(self.x,self.y)
pl.title('connon shell without air resistance')
pl.xlabel('x/R')
pl.ylabel('y/H')
pl.ylim(0.0)
pl.show()
a=cannon_shell()
a.run()
a.show_result()
-
consider the resistance of air
import numpy as np
import math
import matplotlib.pyplot as pl
class cannon_shell:
def __init__(self,time_step=0.1,resis_coeff=4e-5,total_time=30,gravity=9.8,initial_dis=0):
print("enter the angle of the cannon shell ->")
self.rad=float(input())
self.angle=(self.rad/180)*math.pi
print("enter the speed of the cannon shell ->")
self.v=input()
self.B2_m=resis_coeff
self.g=gravity
self.dt=time_step
self.v_x=[self.v*(math.cos(self.angle))]
self.v_y=[self.v*(math.sin(self.angle))]
self.x=[initial_dis]
self.y=[initial_dis]
def run(self):
while(self.y[-1]>=0):
self.x.append(self.x[-1]+self.v_x[-1]*self.dt)
self.y.append(self.y[-1]+self.v_y[-1]*self.dt)
self.v_x.append(self.v_x[-1]-self.B2_m*self.v*self.v_x[-1]*self.dt)
self.v_y.append(self.v_y[-1]-self.g*self.dt-\
self.B2_m*self.v*self.v_y[-1]*self.dt)
def show_result(self):
pl.plot(self.x,self.y)
pl.title('connon shell without air resistance')
pl.xlabel('x/R')
pl.ylabel('y/H')
pl.ylim(0.0)
pl.show()
a=cannon_shell()
a.run()
a.show_result()

(3)
Effects of altitude
- isothermal (constant temperature) ideal gas
which
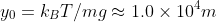
-
adiabatic approximation
which
 -
the drag force due to air resistance is proportional to the density
consider the reduce of air density
import numpy as np
import math
import matplotlib.pyplot as pl
class cannon_shell:
def __init__(self,time_step=0.1,resis_coeff=4e-5,total_time=30,gravity=9.8,initial_dis=0):
print("enter the angle of the cannon shell ->")
self.rad=float(input())
self.angle=(self.rad/180)*math.pi
self.v=700
self.B2_m=resis_coeff
self.g=gravity
self.dt=time_step
self.v_x=[self.v*(math.cos(self.angle))]
self.v_y=[self.v*(math.sin(self.angle))]
self.x=[initial_dis]
self.y=[initial_dis]
def run(self):
while(self.y[-1]>=0):
self.rho=(1-(2.257e-5)*self.y[-1])**2.5
self.x.append(self.x[-1]+self.v_x[-1]*self.dt)
self.y.append(self.y[-1]+self.v_y[-1]*self.dt)
self.v_x.append(self.v_x[-1]-self.rho*self.B2_m*self.v*self.v_x[-1]*self.dt)
self.v_y.append(self.v_y[-1]-self.g*self.dt-\
self.rho*self.B2_m*self.v*self.v_y[-1]*self.dt)
labeltext=str(self.rad)
pl.plot(self.x,self.y,label=labeltext)
def show_result():
pl.title('connon shell without air resistance')
pl.xlabel('x/m')
pl.ylabel('y/m')
pl.ylim(0.0)
pl.legend(loc='upper left')
pl.show()
a=cannon_shell()
b=cannon_shell()
c=cannon_shell()
d=cannon_shell()
e=cannon_shell()
f=cannon_shell()
a.run()
b.run()
c.run()
d.run()
e.run()
f.run()
show_result()
show the result

(4)