本文主要是对《R语言实战》第五章的实践练习,参考本职工作中经常需要用到的绘制产品质量控制图,看了第五章后,发现里面用到的一些统计学函数可以用在产品质量控制图。因此,就以本文加强自己的练习。
一、目的
假设产品尺寸要求是148~150mm,分析产品的Cpk,和绘制产品的均值-极差图,通过Cpk和均值-极差图分析该产品的质量是否属于可控制范围,也就是说产品是否出现质量问题。
二、数据处理步骤
1.生成数据
由于目前没有实际数据在手,所以用了随机函数,生成所需要的服从正态分布的函数。
生成平均值为150.04、极差为0.5的100个服从正态分布的数据。同时使用了set.seed()函数,让随机生成的数据可以重复。

2.将数据由向量转换成矩阵
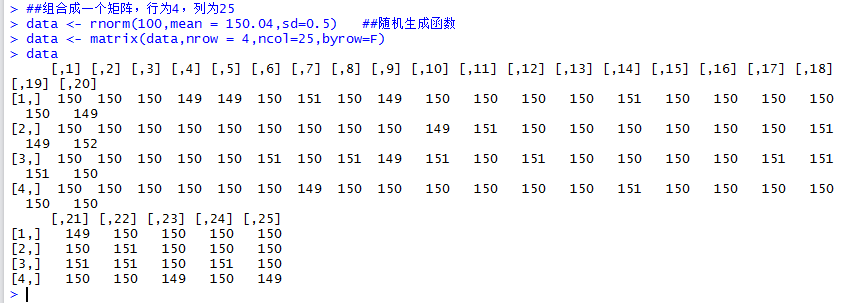
3.对数据进行计算
计算每一列的均值,然后再计算均值的均值:

计算每一列的极差,然后在计算极差的均值:

计算标准差:

计算Cpk,计算Cpk之前,需要计算CpUCL和CpLCL,然后这两者的最小值就是Cpk。其中:
CpUCL=(规格上限-平均值)/(3标准差)
CpLCL=(规格上限+平均值)/(3标准差)
且,产品的Cpk≥1.33方可以接受。

随机生成的数据,产品的Cpk等于1.33,处于刚好到达临界值。
计算均值图的上下限:


计算极差图的上下限:

三、绘制数据分析图
1.绘制均值图
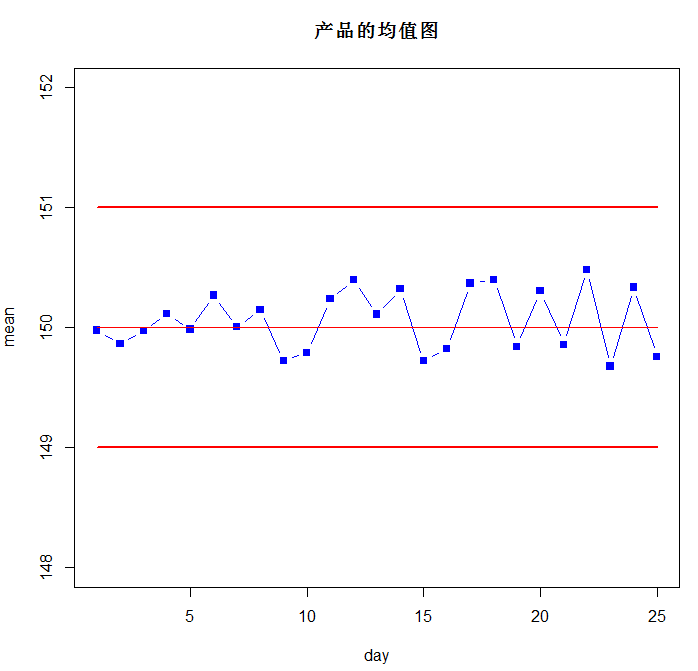
从图中可以看出来,数据没有超出上下限,且没有连续7个点落在同一边,均值附近的点也不多,产品尺寸在可控制的范围内。
2.绘制极差图

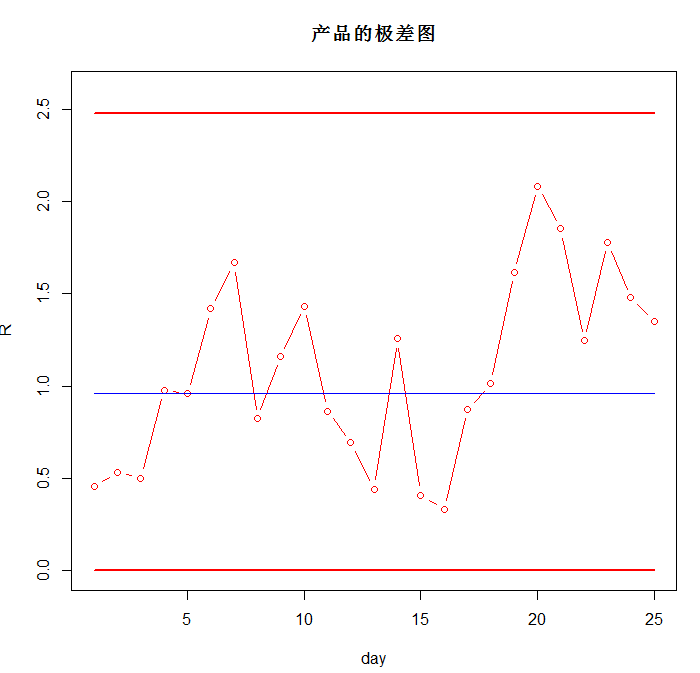
从图中可以看出,后面的八个数字在均值的一边,属于异常数据,需要进一步进行原因分析。
3.将两个图组合在一起


接下来,就需要考虑异常数据的分析~
总结:
第一次将R语言运用在工作中,之前都是用的Excel完成的,利用R语言后,发现相对来说要简单多了,不需要将数据一个个套用公式,而且数据可视化这点也比用Excel方便很多。接下来继续找数据练习~