- 这次是上次炮弹射击的升级版,要求考虑发射角度误差,速度误差和迎面风阻误差
- 发射角度误差为正负2度,速度误差为正负5%,迎面风阻误差为正负10%
- 如果要精确打击到指定点,我的想法是应当先设置好炮弹射击的初始参数,即初始速度
公式推演
1
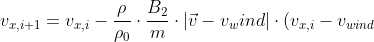\cdot\Delta t \ \approx v_{x,i}-\frac{\rho}{\rho_0}\cdot\frac{B_2}{m}\Delta v\cdot v_{x,i}\cdot \Delta t)
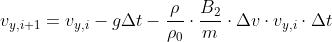
2
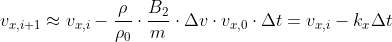
其中
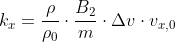
\cdot\Delta t=v_{y,i}-k_y\Delta t)
3
设定发射距离为dis和时间t,则有:
解得:
且:
解得:
但考虑到k_x里有参数v_x0,k_y里有参数v_y0
则有:
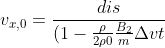t})
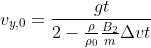
但由于:
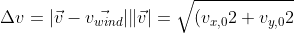})
这个参数不太好弄,所以我令:
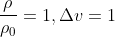
任性=_=
code(python 2.7)
import numpy
import math
import random
import matplotlib.pyplot as pl
class cannon_shell:
def __init__(self,time_step=0.001,resis_coeff=4e-5,total_time=30,gravity=9.8,initial_dis=0):
print("enter the distance what you want to get ->")
self.distance=float(input())
print("enter the time to get ->")
self.t=float(input())
print("enter the velocity of wind ->")
print("1.v_wind > 0 means tailwind")
print("2.v_wind < 0 means headwind")
self.v_wind=float(input())
self.B2_m=resis_coeff
self.g=gravity
self.dt=time_step
self.rho=1
self.ini_vx=self.distance/((1-0.5*self.rho*self.B2_m*self.t)*self.t)
self.ini_vy=(self.g*self.t)/(2-self.rho*self.B2_m*self.t)
self.v_x=[self.ini_vx]
self.v_y=[self.ini_vy]
self.v=(pow(self.v_x[-1],2)+pow(self.v_y[-1],2))**0.5
self.sin=self.v_y[-1]/self.v
self.theta=float((180*math.asin(self.sin))/math.pi)
self.x=[0]
self.y=[0]
def re_init(self):
self.v_x=[self.ini_vx]
self.v_y=[self.ini_vy]
self.v=(pow(self.v_x[-1],2)+pow(self.v_y[-1],2))**0.5
self.sin=self.v_y[-1]/self.v
self.theta=float((180*math.asin(self.sin))/math.pi)
self.x=[0]
self.y=[0]
def run(self):
vran=self.v
thetaran=self.theta
self.v=random.uniform(vran*0.95,vran*1.05)
self.theta=random.uniform(thetaran-2,thetaran+2)
self.v_x=[self.v*math.cos((self.theta/180)*math.pi)]
self.v_y=[self.v*math.sin((self.theta/180)*math.pi)]
while(self.y[-1]>=0):
self.rho=(1-(2.257e-5)*self.y[-1])**2.5
self.v=(pow(self.v_x[-1],2)+pow(self.v_y[-1],2))**0.5
self.deltaV=(pow(self.v,2)-2*self.v*self.v_wind+pow(self.v_wind,2))**0.5
self.x.append(self.x[-1]+self.v_x[-1]*self.dt)
self.y.append(self.y[-1]+self.v_y[-1]*self.dt)
self.v_x.append(self.v_x[-1]-self.rho*self.B2_m*self.deltaV*\
(self.v_x[-1]-self.v_wind)*self.dt)
self.v_y.append(self.v_y[-1]-self.g*self.dt-\
self.rho*self.B2_m*self.deltaV*self.v_y[-1]*self.dt)
'''labeltext=str(self.rad)'''
def show_result(self):
labeltext="shoot point="+str(self.x[-1])+\
" "+"velocity="+str((pow(self.v_x[0],2)+pow(self.v_y[0],2))**0.5)
pl.plot(self.x,self.y,label=labeltext)
pl.title('connon shell with air resistance')
pl.xlabel('x/m')
pl.ylabel('y/m')
pl.ylim(0.0)
pl.legend(loc='upper left')
pl.show()
def calTrajectory():
Delta_x=[]
a=cannon_shell()
for i in range(200):
a.run()
Delta_x.append(a.x[-1]-a.distance)
a.re_init()
AverDelta=sum(Delta_x)/200
a.ini_vx=a.ini_vx-AverDelta/a.t
a.re_init()
a.run()
a.show_result()
calTrajectory()
结果
误差还是蛮大的,我不想上台比试U_U
- 能力有限,就只能做到这里了2333
- 还没有考虑迎面风阻误差
- 心累