本文为翻译,个人学习之用,原地址
程序状态
如果你以前有其他语言的编程经验,你可能写过一些函数或者方法来控制程序的状态。概念化的话,状态就是当执行一些计算过程的时候,所必须的一个或者多个变量,而且这些变量跟函数的参数没有关联。面向对象的语言,比如C++,就以成员变量的形式广泛地使用了状态变量。C语言中,我们在函数的作用域外声明变量来保持状态。
在Haskell中,这种技术就没那么容易直接应用了。因为必须要使用变量,意味着函数会隐藏掉一些依赖。这与Haskell的纯函数(参数相同,函数每次调用结果一致)相违背。
幸运的是,在大多数情况下,我们可以避免这种额外的计算,然后使用纯函数的方式来跟踪程序状态。我们通过传递状态信息来做到这点,这样那些隐藏的依赖就会变得明确了。
State类型就是一个精心设计,让这个过程更加便利的工具。在这章中,我们会从一个典型的问题(产生伪随机数)中引进state,来展示它是怎样帮助我们的。
伪随机数
生成真正的随机数是很困难的。计算机程序大多数情况下会使用伪随机数来代替。之所以称之为“伪”,是因为它们并不是真正的随机。它们使用算法(伪随机数生成器)生成,这种算法需要一个初始状态(通常叫做种子),然后根据这个状态来产生一系列貌似随机的数字。每次产生随机数的时候,这个状态就必须要更新,伪随机数生成器就会刷新,如果知道了初始种子和生成算法,不同的伪随机数序列是可以重现的。
在Haskell中的实现
在大多数编程语言中,生成伪随机数非常简单:在库中就已经提供了生成伪随机数的函数。(甚至是真正的随机数,取决于其实现)。Haskell也不例外,在random包中的System.Random模块中也有这个方法:
GHCi> :m System.Random
GHCi> :t randomIO
randomIO :: Random a => IO a
GHCi> randomIO
-1557093684
GHCi> randomIO
1342278538
randomIO是一个IO action。它也不例外,使用一个可变的状态。因为这个隐藏的依赖,这个函数生成的伪随机数每次都是不同的。
例子:掷骰子
假定我们在写一个掷骰子的游戏,我们创建一个掷骰子的方法。我们使用IO函数randomRIO,它允许我们指定一个随机数的范围。对于六面筛子,randomRIO (1, 6).
import Control.Monad
import System.Random
rollDiceIO :: IO (Int, Int)
rollDiceIO = liftM2 (,) (randomRIO (1,6)) (randomRIO (1,6))
这个方法会掷骰子两次,(,)是个函数,接受两个参数,返回一个二维元组,liftM2 让(,)函数能够接受monadic参数。这样,这个函数会返回一个IO元组。
练习
实现一个函数rollNDiceIO :: Int -> IO [Int],需要一个整型数(掷骰子次数),返回一个随机数列表,范围1-6
去掉IO
randomRIO 一个缺点是,它必须使用IO,将我们的状态保存在程序外,我们并不能控制它。我们尽量只在必须要与外部世界交互的时候使用I/O。
为了避免使用IO,我们创建一个本地的生成器。在System.Random包中的 random和mkStdGen函数允许我们生成一个元组,其中包含伪随机数和一个更新过的生成器,以备下次这个函数下次调用。
GHCi> :m System.Random
GHCi> let generator = mkStdGen 0 -- "0" is our seed
GHCi> :t generator
generator :: StdGen
GHCi> generator
1 1
GHCi> :t random
random :: (RandomGen g, Random a) => g -> (a, g)
GHCi> random generator :: (Int, StdGen)
(2092838931,1601120196 1655838864)
注意
在random generator :: (Int, StdGen)中,我们使用::来引进类型注解,本质上就是一个类型签名。我们可以认为random generator是(Int, StdGen)类型。random可以产生不同类型的值,如果我们想要Int类型,我们最好通过类型签名指定。
我们设法避免IO,但这里又有一个新问题。首先,如果我们要使用generator获取一个随机数,明显我们定义...
GHCi> let randInt = fst . random $ generator :: Int
GHCi> randInt
2092838931
...是毫无用处的。它总是返回相同的值,2092838931,因为每次都是相同的生成器在相同的状态。为了解决这个问题,我们可以使用元组的第二个成员(就是那个生成器),然后传递给新调用的random:
GHCi> let (randInt, generator') = random generator :: (Int, StdGen)
GHCi> randInt -- Same value
2092838931
GHCi> random generator' :: (Int, StdGen) -- Using new generator' returned from “random generator”
(-2143208520,439883729 1872071452)
这样看起来好笨,而且相当啰嗦。
不使用IO的掷骰子
我们使用一种新方法来掷骰子,randomR函数:
GHCi> randomR (1,6) (mkStdGen 0)
(6, 40014 40692)
结果包含了一次掷骰子的结果和一个新的生成器。掷两次骰子的实现:
clumsyRollDice :: (Int, Int)
clumsyRollDice = (n, m)
where
(n, g) = randomR (1,6) (mkStdGen 0)
(m, _) = randomR (1,6) g
练习
实现rollDice :: StdGen -> ((Int, Int), StdGen)函数,接受一个生成器,返回一个包含两个随机数的元组和一个生成器。
clumsyRollDice 执行一次就能得到我们想要的结果,但是,我们必须手动传入生成器g。它会随着我们的程序的复杂变得越来越笨重。而且非常容易出错:如果我们将中间的生成器传入到一个错误的where从句中了呢?
我们真正需要的是一种能自动地提取元组的第二个参数,然后传递给新一次的random调用中。所以State 来了。
State 介绍
注意
在本章中,我们使用Control.Monad.Trans.State模块transformers包中的state monad。通过广泛阅读Haskell代码,你会遇到Control.Monad.State,一个和mtl包密切相关的模块。这两个模块之间的区别现在可以不用关心:我们讨论的都是应用在mtl的变种。
Haskell类型State 描述一个函数,这个函数消费一个state,产出一个二维元组,包含结果和一个更新过的state。
这个状态函数封装了一个定义了runState访问器的数据类型。这样就不用使用模式匹配了。对于当前目的,这个State类型应该定义成:
newtype State s a = State { runState :: s -> (a, s) }
这里,s是state的类型,a是产出结果的类型。把它叫做State类型可能有些不恰当,因为封装的值并不是state本身,而是一个state处理器。
newtype
注意,我们使用newtype关键字定义这个数据类型,而不是data。newtype只能有一个数据构造器和一个字段。这样保证了可以使用编译器来做封装和解封这个单个字段的工作。出于这个原因,我们通常使用newtype来定义State。使用type来定义一个别名能否满足需求呢?答案是否定的,因为type不允许我们为一个新数据类型定义实例,这与我们的目的背道而驰。
State构造器在哪?
当你开始使用Control.Monad.Trans.State,你很快会注意到并没有可用的State构造器。这就是我们在前几段介绍这个类型时,“我们当前目的” 警告的原因。transformers包以一种不大相同的方式实现了State类型。这些差别并不影响我们使用和理解State;除了这个,Control.Monad.Trans.State导出了state函数,来替代State构造器,做了同样的工作。
state :: (s -> (a, s)) -> State s a
至于实现为什么不显而易见,我们接下来介绍。
实例化Monad
到目前为止,我们所做的仅仅是包装了一个方法,然后给它命名。还有另外一个任务,State是一个monad,提供给我们很便利的方式去使用它。不像我们以前见过的Functor和Monad实例,State有两个类型参数。因为类型类只允许一个类型参数,因此我们要指出另外一个,s。
instance Monad (State s) where
这意味着有很多不同的State monad,每种类型都有可能成为state- State String,State Int,State SomeLargeDataStructure,等等。当然,我们需要实现return和(>>=)方法;这些方法能够处理所有s取值的情况。
return函数实现:
return :: a -> State s a
return x = state ( \ st -> (x, st) )
给定一个值 (x)到return得到一个函数,这个函数接受一个state (st),并将其和一个我们想要返回的值一起返回。最后一步,这个函数被一个state函数包裹起来。
绑定函数有一些绕:
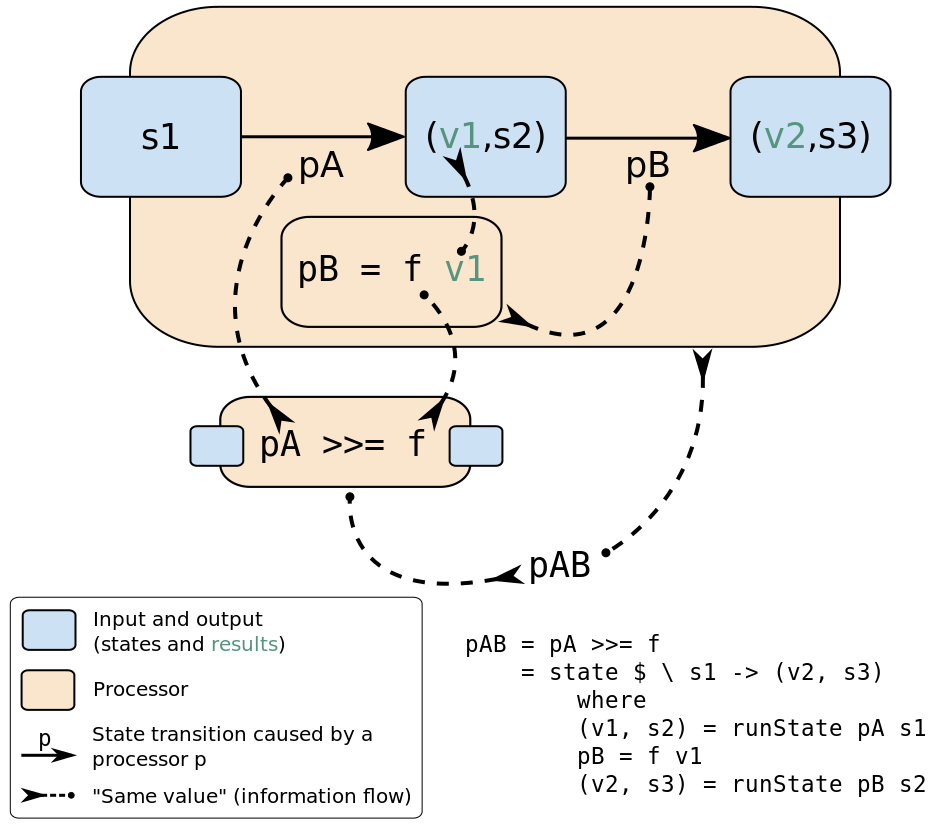
(>>=) :: State s a -> (a -> State s b) -> State s b
pr >>= k = state $ \ st ->
let (x, st') = runState pr st -- Running the first processor on st.
in runState (k x) st' -- Running the second processor on st'.
(>>=) 需要两个参数,一个state处理器和一个根据第一个结果创建出另外一个处理器的函数k。两个处理器在一个接受初始化state (st)并返回第二个结果和第三个state的函数中结合(这句话可能有问题),总之,(>>=)允许我们依次运行两个state 处理器,第一阶段的结果会影响到第二个阶段的结果。
一个实现的细节是runState在State的包裹下是怎样使用的,我们深入到这个应用到state上的函数中去。runState pr,是s -> (a, s)的实例。
设置和访问State
monad实例让我们能够操作各种state 处理器,但是在此时,你可能很好奇,那个最原始的state是来自哪的。这个问题是由put函数处理:
put newState = state $ \_ -> ((), newState)
给定一个state(我们想要引进的那个),put生成了一个state处理器,忽略它接收到的任何state,然后发挥返回提供给put的state。由于我们不关心这个处理器的结果(我们要做的是替换这个state),元组的第一个元素会是(),一个占位的值。
get = state $ \st -> (st, st)
结果state处理器返回state st,会被作为一个结果同时也作为一个state返回。这就意味着这个state将不会改变,并且提供一个副本供我们操作。
获取值和State
我们已经实现了(>>=),runState解包State a b,来获取真正的state处理函数,这个函数接着会应用于一些初始state。还有其他相似用途的函数比如evalState和execState。提供一个State a b和一个初始state,evalState会只返回state处理后的结果,execState只返回新的state。
evalState :: State s a -> s -> a
evalState pr st = fst (runState pr st)
execState :: State s a -> s -> s
execState pr st = snd (runState pr st)
掷骰子和state
是时候将State monad应用到我们掷骰子的例子上了。
import Control.Monad.Trans.State
import System.Random
我们希望通过类型StdGen的伪随机发生器产生掷骰子的结果。因此state 处理器的类型是State StdGen Int,跟包装后的StdGen -> (Int, StdGen)一致。
现在我们可以实现的处理器,给定一个StdGen发生器,产生1和6之间的一个数。randomR的类型是:
-- The StdGen type we are using is an instance of RandomGen.
randomR :: (Random a, RandomGen g) => (a, a) -> g -> (a, g)
看起来熟悉吗?如果我们把a看成Int,g看成StdGen,就会变成:
randomR (1, 6) :: StdGen -> (Int, StdGen)
我们已经有了一个state处理函数!现在缺少的是把它包装进state:
rollDie :: State StdGen Int
rollDie = state $ randomR (1, 6)
出于便于理解的目的,我们可以使用get,put和do语法来写rollDie,这样就能很清晰的展示出每一步的处理过程:
rollDie :: State StdGen Int
rollDie = do generator <- get
let (value, newGenerator) = randomR (1,6) generator
put newGenerator
return value
我们来过一遍每一个步骤:
- 第一步,我们使用
<-,从一个monadic 上下文中取出伪随机数生成器,供后边使用。 - 然后,我们使用
randomR函数和上步产生的生成器产生一个1-6的整数。我们把randomR返回的新生成的生成器存储起来。 - 我们接下来使用
put把新的newGenerator设置到state,以至于以后的randomR或者(>>=)链能使用一个不同的随机数生成器。 - 最后,我们使用
return将结果注入到State StdGenmonad中。
最终我们可以使用我们的monadic骰子了。在此之前,初始state生成器本身是由mkStdGen函数生成。
GHCi> evalState rollDie (mkStdGen 0)
6
为什么我们要把monad掺和进来,创建了一个错综复杂的框架仅仅是为了实现这个fst $ randomR (1,6)?好吧,思考下以下函数:
rollDice :: State StdGen (Int, Int)
rollDice = liftM2 (,) rollDie rollDie
我们得到一个可以产生一个包含两个伪随机数的二维元组的函数。注意一下他们的与众不同之处:
GHCi> evalState rollDice (mkStdGen 666)
(6,1)
在其内部,state是通过(>>=)从一个rollDie传递给其他的。而我们原本使用randomR (1, 6)的做法十分笨重,因为我们必须手动的传递state。现在,monad实例帮助我们做这些事情。假定我们知道怎样使用lifting函数,构造复杂的随机数组合(元组,列表或者其他)会突然变得很简单。
不同类型的随机数
到目前为止,我们仅仅通过伪随机数生成器产出了Int类型的值。但是从randomR的类型并不仅限于Int。它可以生成System.Random中Random类中的任何类型的值。已经实现了Int,Char,Integer,Bool,Double和Float,所以你可以生成它们其中的任何一个。
因为State StdGen并不知晓关于生成的伪随机数的类型,所以我们可以写一个相似的函数来提供一个并不指定类型的伪随机数:
getRandom :: Random a => State StdGen a
getRandom = state random
与rollDie相比,这个函数在声明中并不指定Int类型,然后使用random代替randomR;否则的话它们是相同的。getRandom可以用在任何Random实例上。
GHCi> evalState getRandom (mkStdGen 0) :: Bool
True
GHCi> evalState getRandom (mkStdGen 0) :: Char
'\64685'
GHCi> evalState getRandom (mkStdGen 0) :: Double
0.9872770354820595
GHCi> evalState getRandom (mkStdGen 0) :: Integer
2092838931
someTypes :: State StdGen (Int, Float, Char)
someTypes = liftM3 (,,) getRandom getRandom getRandom
allTypes :: State StdGen (Int, Float, Char, Integer, Double, Bool, Int)
allTypes = liftM (,,,,,,) getRandom
`ap` getRandom
`ap` getRandom
`ap` getRandom
`ap` getRandom
`ap` getRandom
`ap` getRandom
对于allTypes,因为没有liftM7(标准库中只到liftM5)我们使用Control.Monad中的 ap函数替代。ap适合多次计算成多参数函数的应用。理解ap函数,看一下它声明:
ap :: (Monad m) => m (a -> b) -> m a -> m b
谨记,在Haskell中,a类型变量可以被函数类型替换,跟这个比较:
GHCi>:t liftM (,,,,,,) getRandom
liftM (,,,,,) getRandom :: (Random a1) =>
State StdGen (b -> c -> d -> e -> f -> g
-> (a1, b, c, d, e, f, g))
很明显,monad m变成了State StdGen,ap的第一个参数是一个函数b -> c -> d -> e -> f -> g -> (a1, b, c, d, e, f, g)。重复应用ap,我们最后得到一个元组,而不是一个函数。把它们加起来,ap把一个在monad中的函数应用于一个monadic值(而liftM/fmap,是把一个不在monad中的函数应用于一个monadic值)。
GHCi> evalState allTypes (mkStdGen 0)
GHCi>(2092838931,9.953678e-4,'\825586',-868192881,0.4188001483955421,False,316817438)