
集成学习
集成学习是什么?集成学习通过训练多个分类器,然后将其组合起来,从而达到更好的预测性能,提高分类器的泛化能力。
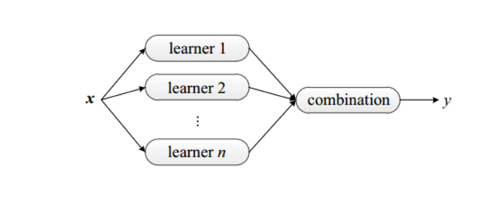
目前集成学习主要有3个框架:bagging,boosting,stacking。
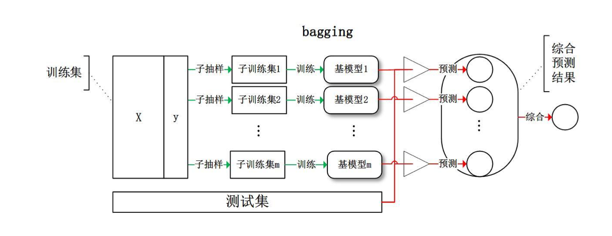
先看第一个bagging:bagging的时候每个分类器都随机从原样本中做有放回的采样,训练基模型,最后根据多个基模型的预测结果产出最终的结果。bagging的一种常见方法是我们训练好多模型:SVM, 决策树,DNN等,然后将最后再用一个lr做组合。
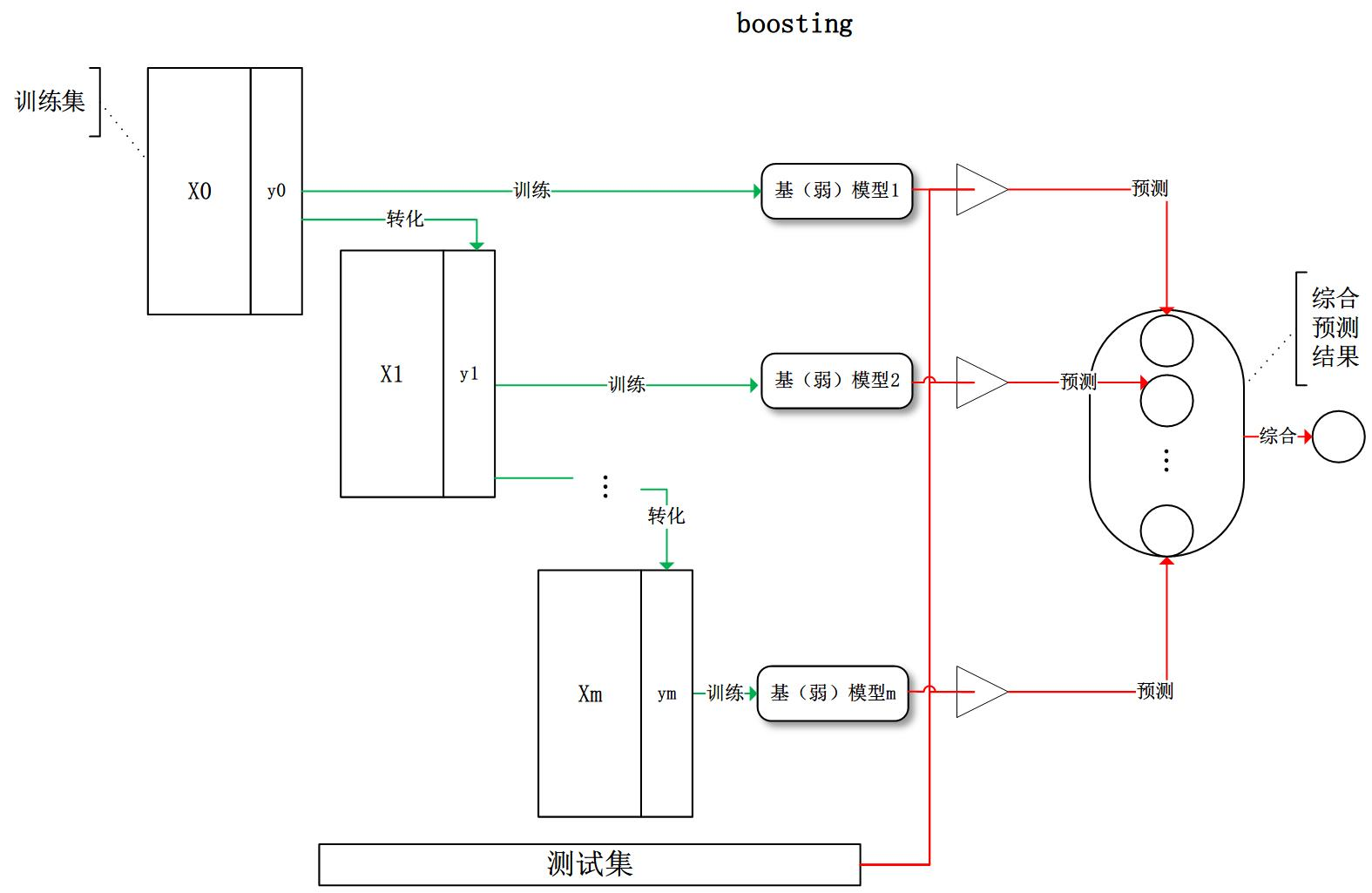
第二个boosting:boosting每次对训练集进行转换后重新训练出基模型,最后再综合所有的基模型预测结果。主要算法有 AdaBoost 和 GBDT。
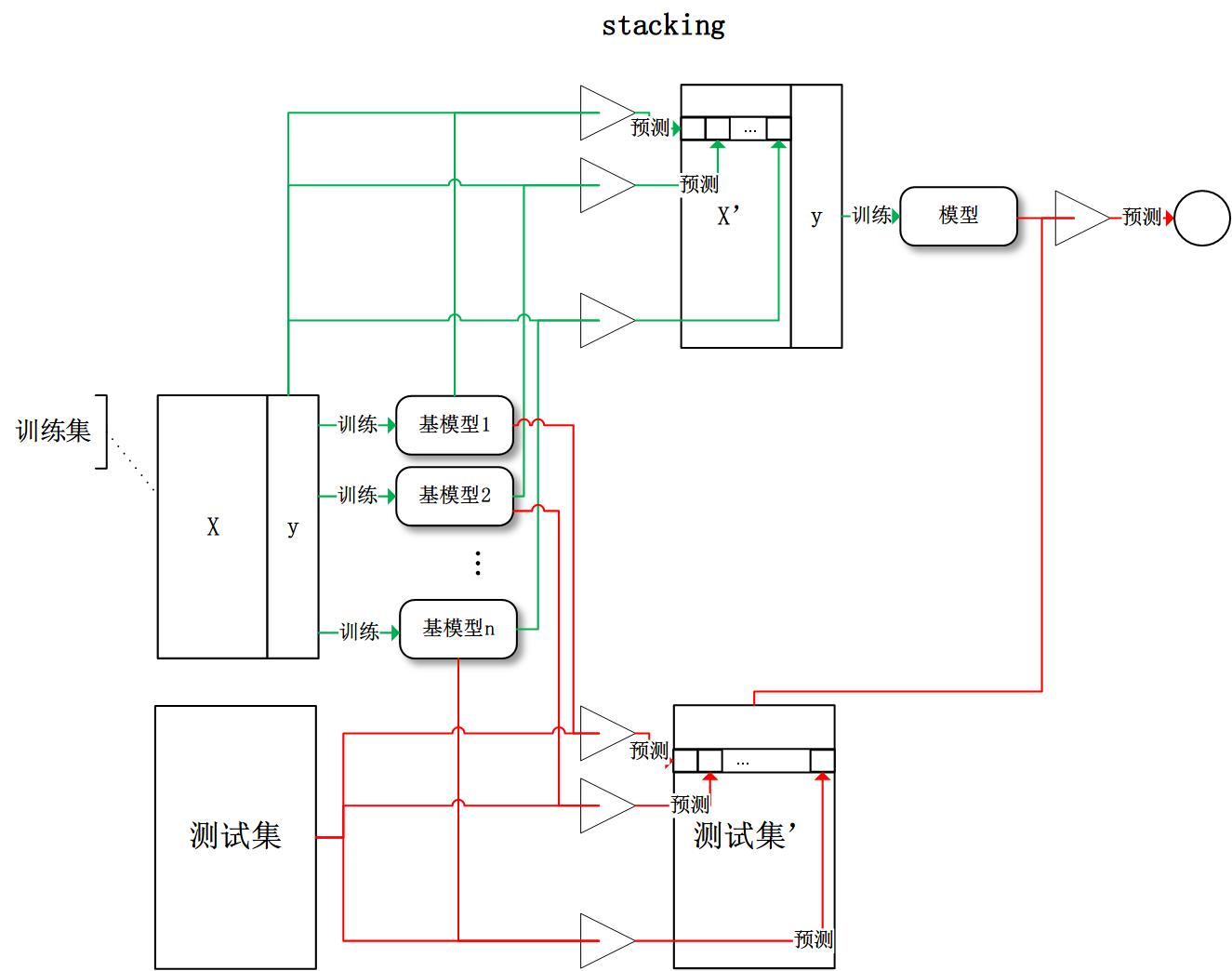
第3个stacking:stacking的思想是将每个基模型的输出组合起来作为一个特征向量,重新进行训练。
在学习集成学习中,我们需要知道一个非常重要的概念:Diversity,我们希望每个基模型都不尽相同,这样子最后的预测结果才能好。
xgboost详解
假设我们最后的预测函数形式如下:
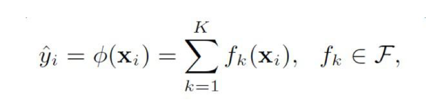
最终的预测结果由K颗树集成所成,接着我们定义要优化的目标函数:
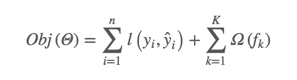
目标函数由两部分组成:第一部分是训练损失,第二部分则是每颗树的复杂度,复杂度的衡量有多种方法:树的深度,内部节点个数,叶子节点个数(T),叶节点分数(w),xgboost使用了:
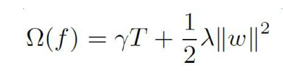
我们将预测函数稍微做个展开:

第t次迭代后,模型的预测等于前t-1次的模型预测加上第t棵树的预测,此时的目标函数:

此时我们将目标函数做二阶泰勒展开:
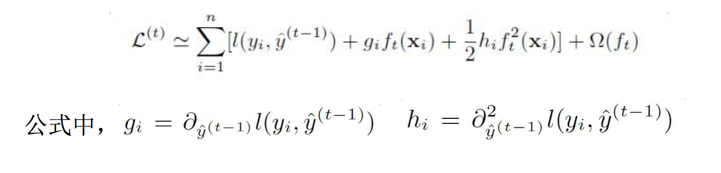
此时第一项是一个常数项,重新整理目标函数得到:
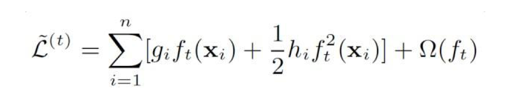
上式中误差函数和正则项分别是:
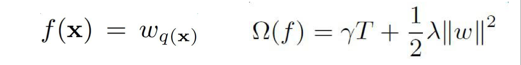
将其带入目标函数,并整理得到:
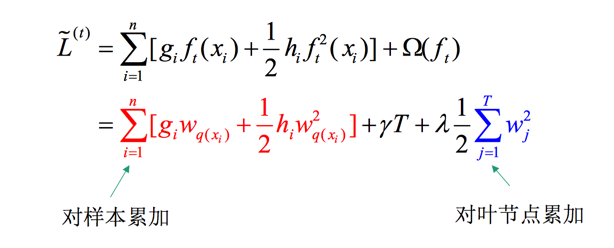
此时我们考虑将对样本的累加和对叶子节点的累加统一到节点的累加,定义下面的函数:

此处我们假设了树的结构是固定的,于是对目标函数求导后可得:
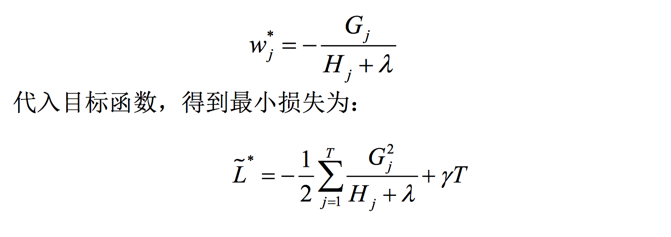
到这一步:我们已经推导出其最优的叶节点分数以及对应的最小损失值,下一步需要解决的问题是:怎么确定树结构。
我们尝试着计算分裂后树的增益,选择增益最大的点进行分裂,在计算增益上,ID3算法采用信息增益,C4.5算法采用信息增益比,CART采用Gini系数,xgboost采用:
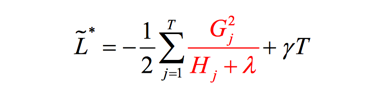
分裂前后的增益定义:
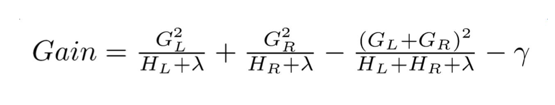
再有的优化就是对于怎么快速计算树结构了,网上内容很多,不再详述了。
adaboost 推导

此时我们对损失函数对参数beta求导,可得
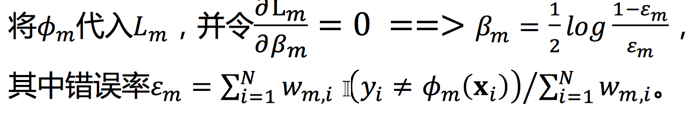
gbdt
梯度提升算法:首先给定一个损失函数L(y,F(x)),其输入是训练对:(x1,y1),(x2,y2),...,(xn,yn),目标是找到最优的F(x),使得损失函数L最小,按照传统梯度下降的方法,我们会将训练数据(xi,yi)带入,然后求L对参数的偏导,再用负梯度进行参数更新:

这么做的一个前提是我们需要保证损失函数对F可微,F对参数 $\theta$可微,第二个可微可以说比较困难,于是我们退而求此次直接求对于F的梯度(函数空间):
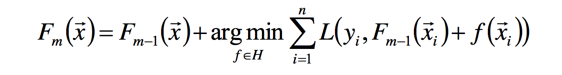
此时f可以用梯度下降的方法,求损失函数在$F_{m-1}$的导数,可得到:
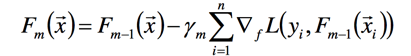
此时我们假设$F_{m-1}$和$y_i$都是已知的,则只有$\gamma_m$是未知的,通过一维的线性搜索就可以找到最优的值:
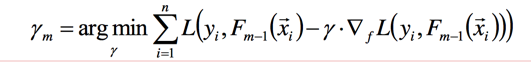
通过上面的讲述,我们将通过(x,y)来求未知参数$\theta$,转换为通过$(x,\nabla_f(y_i,F_{m-1}))$来预估第m颗树$f$,整个过程总结如下:

下一篇将通过代码来详细介绍本篇的算法,尽请期待。
参考
使用 sklearn 进行集成学习——理论
GBDT算法原理与系统设计简介
小象学院《机器学习》课程