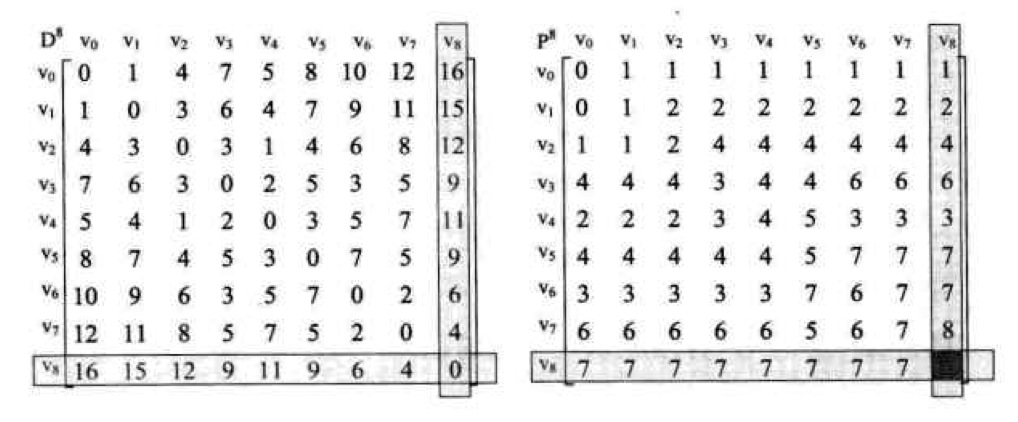
图_最短路径(个人认为应该叫最佳路径)
最短路径其实说的是权重,请仔细理解权重的意义。在实际应用中,权重可以是消耗的时间、金钱、距离甚至是概率等等,我们求最短路径,也就是求这些权重之和的最小(或最大)值
北京地铁复杂的线路图,从育新小区到公益西桥有很多条线路可以选择,从时间、距离、还有车费等不同的角度考虑,可能获得的最佳线路都不一样~~~
迪杰斯特拉(Dijkstra)算法
(两个顶点之间的最短路径)
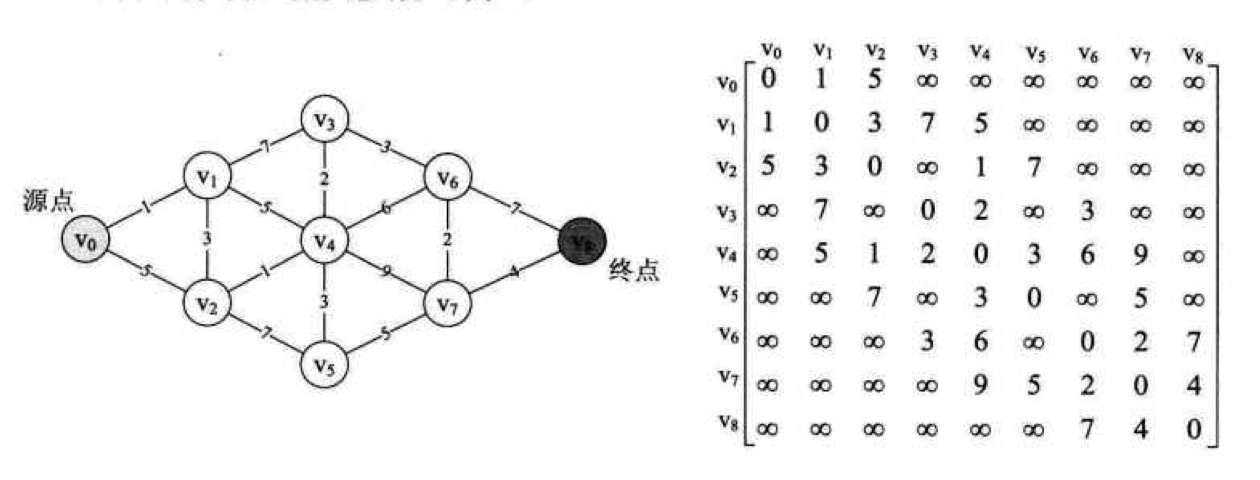
按照路径长度递增的产生最短路径的算法,也就是说不是一次性算出两个定点之间的最短距离,而是通过计算每个中间顶点的最短距离,最后推导出要求的顶点最短距离


- 5~12行是初始化阶段,final一维数组值均为0,D数组记录所有顶点到v0的最短路径值,当前是{65535,1,5,65535,65535,65535,65535,65535,65535},p数组全为0,表示目前还没有找到任意一个顶点的最短路径
- 13行是一个主循环,每循环一次求得v0与一个顶点的最短路径,也就是让一个顶点的final值为1
- 16~24行的循环,先令min为65535,通过w循环,与D[w]比较,找到目前最小的min和k值。当前是:D[1]的值最小,因为在第一次初始化的时候,v0连接的就两条边,v1和v2,如果是第二次循环,那就是D[2]
- 25~32行,是在修正之前已经判定的v0和某个点的最短距离,例如:在初始化的时候v0到v2的最短距离是5,但是第一次循环完成之后,发现v0->v1=min=1,v1->v2=3,因此v0->v1->v2=min+G.matirx[v1][v2]=4,这个值是小于D[2]=5的
佛洛伊德(floyd)算法
能计算出北京地铁所有站与站之间在时间上的最佳路径,那所有上班族就知道该怎么换乘才最省时间!!!
(所有顶点到其他顶点之间的最短距离)
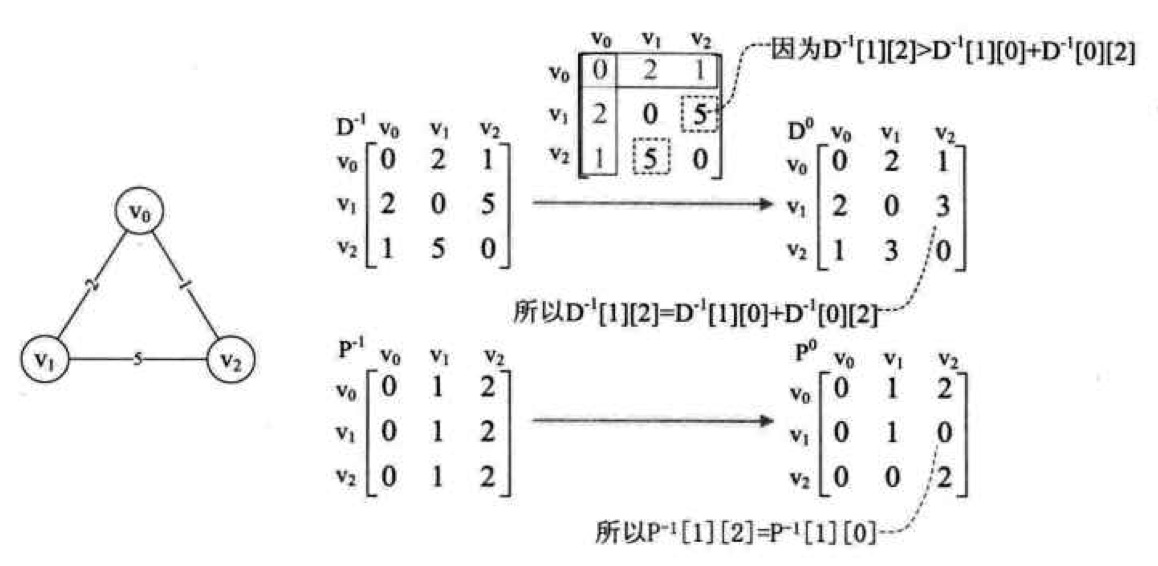
上面这个公式的含义就是:我们要判断所有顶点经过k顶点到达另一个顶点的最短路径。例如:v->w > v->k->w,整个算法就是根据这个简单的逻辑推导出所有顶点到其他顶点的最短路径,看看下面的图:
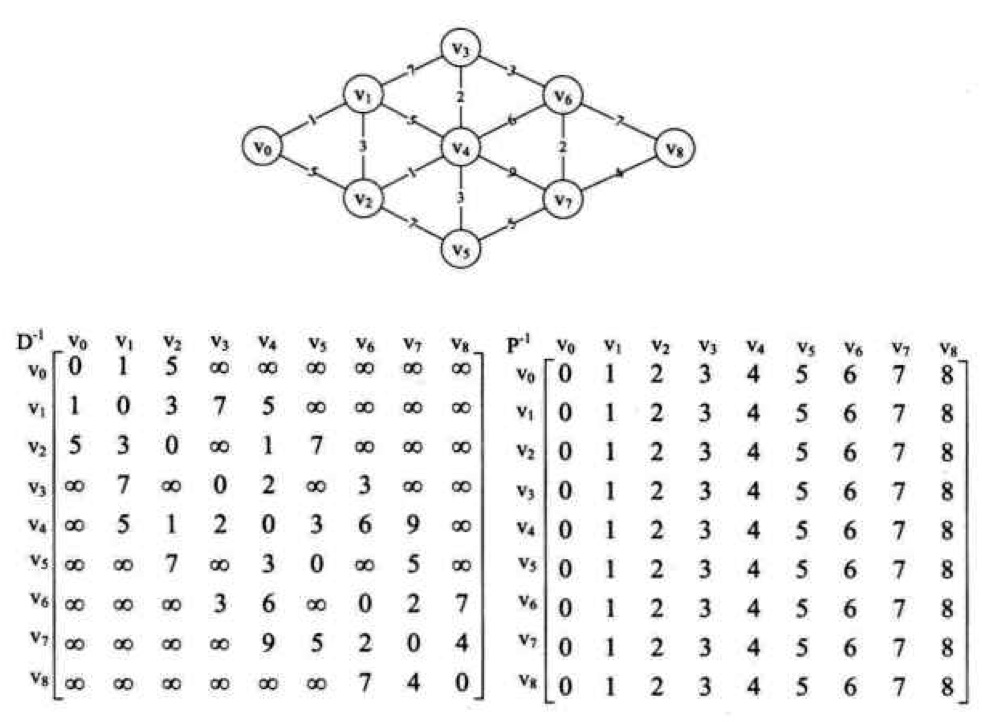
代码


该算法用一个三层的循环遍历了所有的顶点,并计算出了顶点与顶点之间的最短距离
其中: k代表中转顶点、v代表起始点、w代表结束顶点
可以通过下面的图形理解k,v,w是怎么运作的
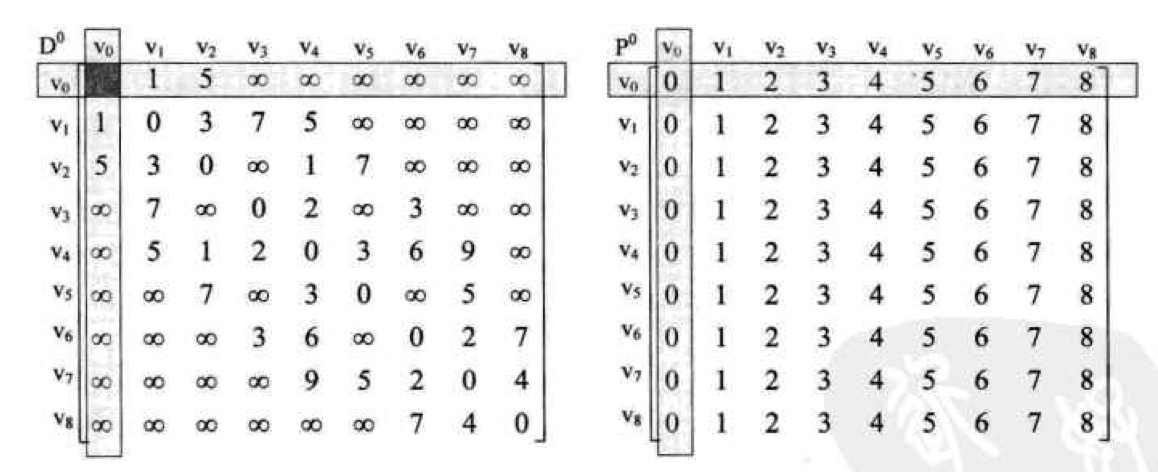
这是v0作为中转顶点时,其他所有顶点通过它到结束点的最短路径,发现不需要更新
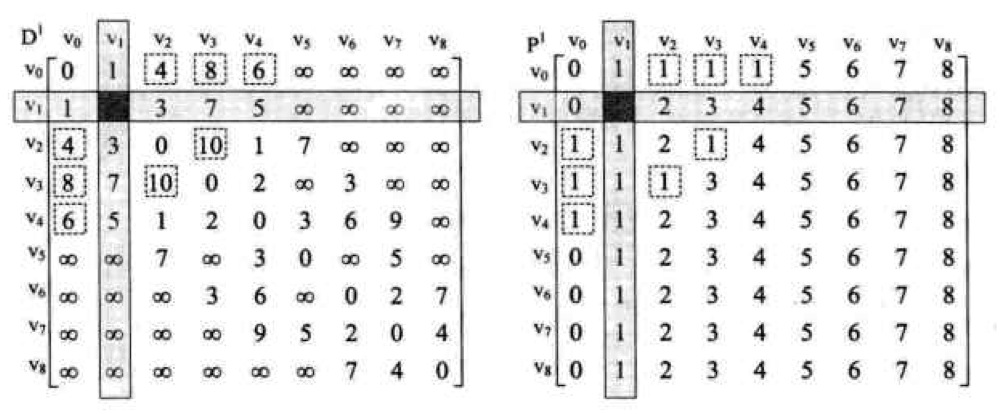
这是v1作为中转顶点,可以看出,例如:原来v0->v2=5,而现在v0->v1->v2=1+3=4,因此我们就需要改变v0->v2的最短路径为4,其他的同理。
就如同上面两步一样,循环进行直到所有顶点被处理一边,最后结束得到的就是所有顶点到顶点之间的最短路径